2520 sayısı 1’den 10’a kadar olan sayıların hepsine kalansız bölünebilen en küçük sayıdır.
1’den 20’ye kadar olan sayıların hepsinekalansız bölünebilenen küçük sayı hangisidir?
Algoritma:
Asal çarpan nedir?
Asal çarpan, bir sayıyı bölen ve asal olan çarpanlardır. Örneğin, 10 sayısının asal çarpanları 2 ve 5’tir.
Bir sayıyı asal çarpanlarına ayıran fonksiyonu yazmak için:
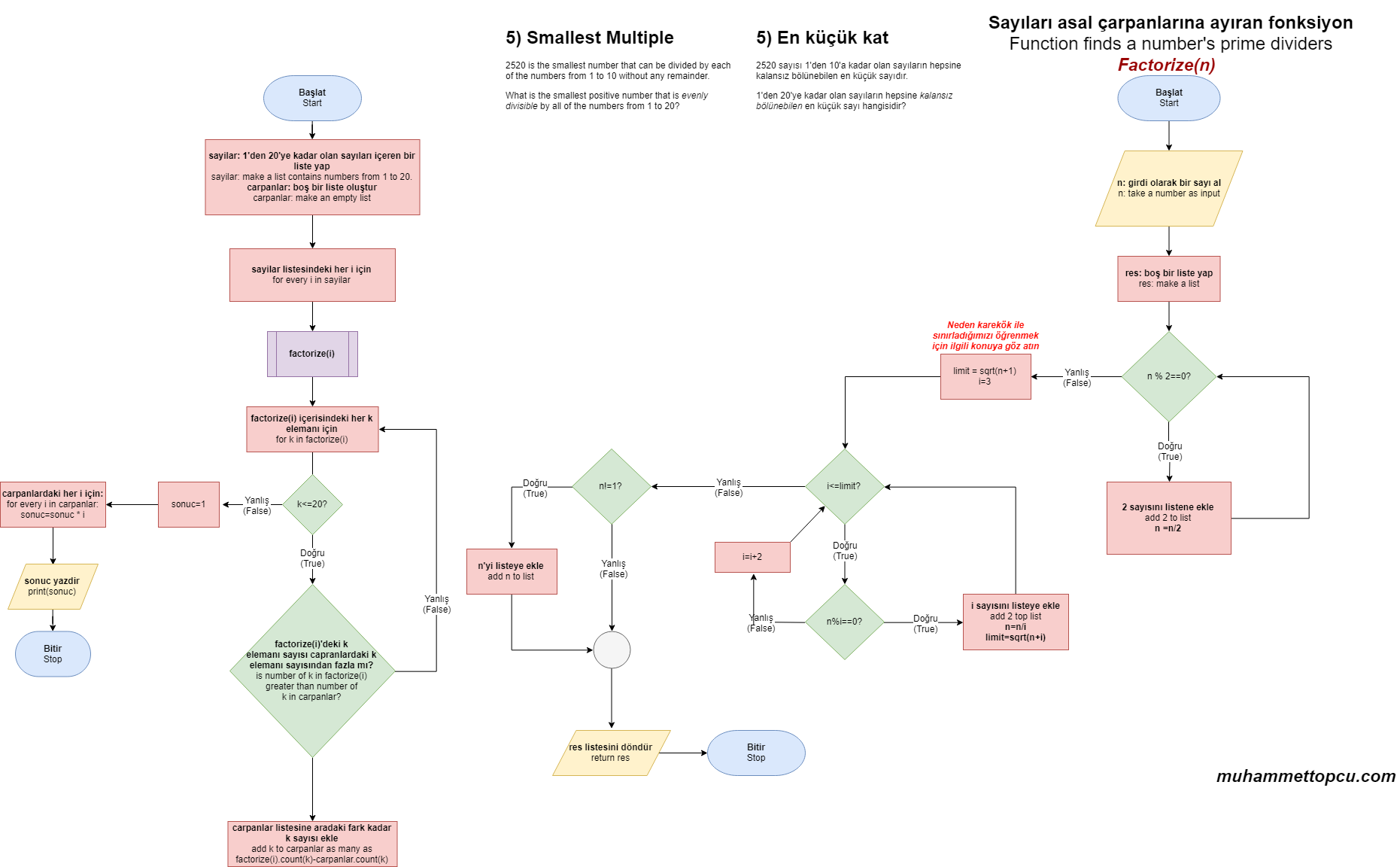
Öncelikle istenilen sayı alınmalı ve en küçük asal sayı olan 2’ye bölünüp bölünmediği kontrol edilmelidir. Sayı ikiye bölündüğü kadar bölünmeli, aynı sayı da iki rakamı önceden belirlenen asal çarpanlar listesine eklenmelidir. Sayı ikiye bölünmediği takdirde, asal çarpan olarak test edilecek sayıların sınırını belirleyen bir üst limit hazırlanmalıdır, bu üst limit şu mantığı içerir:
Kanıt: Elimizde pozitif bir n sayısı olsun ve bu n sayısının çarpanları, birer asal sayı olan p ve q olsun: “n=p.q” Farz edelim ki p>√n ve q>√n olsun. Bu iki eşitsizliği çarptığımızda şöyle bir şey elde ederiz: p.q>√n.√n, ki bu da p.q>n anlamına gelir. Başlangıçtaki n=p.q hipotezimize terstir bu. O hâlde buradan şu çıkarımı yaparız, n sayısının asal çarpanlarından birisi, ya p≤√n ya da q≤√n, sayının kare kökünden küçüktür. O hâlde bir sayının asal çarpanlarını ararken, o sayının kare kökünden küçük sayılara bakmamız yeterlidir.
- i, sıradaki asal sayı olan 3’ten başlayarak, üst limit olarak tanımlanmış (n+1)’in kare köküne kadar olan sayılara kadar denenir.
- 2 sayısında yaptığımız gibi, sayı i’ye bölünebiliyorsa, i sayısı çarpanlar listesine eklenir, sayı i sayısına bölünerek küçültülür, limit (n+i)’nin kare köküne sabitlenir, işlem yapılabildiği kadar tekrarlanır.
- Eğer sayı i’ye bölünemiyorsa, i sayısı 2 arttırılır. (Bunun sebebi, 2’den başka çift asal sayının bulunmayışıdır.)
- i sayısı limiti aştığında, en son n sayısının 1’den farklı olup olmadığı kontrol edilir. Eğer sayı birden farklıysa, yukarıdaki kural gereği son sayının asal olması gerekir, bu sebeple n sayısı da çarpanlar listesine eklenir. Eğer sayı 1 ise, program sonlandırılır. Bütün asal çarpanlar bulunmuş olur.
Şimdi sayıları asal çarpanlarına ayıran bir kod yazdığımıza göre, artık 1’den 20’ye kadar olan sayıların hepsini asal çarpanlarına ayırmalıyız. Ancak şöyle bir durum var. Bu sayılar arasında ortak çarpanı olan sayılar da var. Örnek vermek gerekirse, 2’nin ve 4’ün asal çarpanlarını çarpanlar listesine eklediğimizde, fazladan bir 2 çarpanı eklemiş olacağız. Bu da en küçük katı bulmamıza engel teşkil ediyor. O hâlde bizim bu sayıları eklemeden önce bir denetime tabi tutmamız gerekir. Bunu da, asal çarpanlarını test ettiğimiz sayının çarpanların, çarpanlar listesinde bulunup bulunmadığına bakıp, eksik olan kadarını ekleyerek çözebiliriz. Yani:
- 1’den 20’ye kadar olan sayıları içeren, sayilar listesi oluşturulur.
- Bu listenin içerisindeki tüm sayılar, yukarıda tanımladığımız fonksiyon yardımıyla asal çarpanlarına ayrılır.
- İlgili sayının asal çarpanlarının, çarpanlar listesindeki sayısı kontrol edilir.
- Eğer bu asal çarpanın sayısı, çarpanlar listesindeki miktarından fazlaysa, o hâlde aradaki fark kadar çarpan, çarpanlar listesine eklenir
- Tüm işlemler bittiğinde, çarpanlar listesindeki tüm sayılar, birbirleriyle çarpılır ve en küçük kat bulunmuş olur.
Akış Şeması:
Kod Dökümü:
#pozitif tüm çarpanlarını bulmak
import math
def factorize(n): #bu fonksiyon sayının çarpanlarını verir.
if n == 1:
return [] # special case
res = []
# iterate over all even numbers first.
while n % 2 == 0:
res.append(2)
n //= 2
# try odd numbers up to sqrt(n)
limit = math.sqrt(n + 1)
i = 3
while i <= limit:
if n % i == 0:
res.append(i)
n //= i
limit = math.sqrt(n + i)
else:
i += 2
if n != 1:
res.append(n)
return res
sayilar=[i for i in range(1,21)]
carpanlar=[]
for i in sayilar:
#print(factorize(i))
for s in factorize(i):
if factorize(i).count(s)>carpanlar.count(s):
for i in range(1, factorize(i).count(s)-carpanlar.count(s)+1):
carpanlar.append(s)
sonuc=1
for i in carpanlar:
sonuc*=i
print(sonuc)