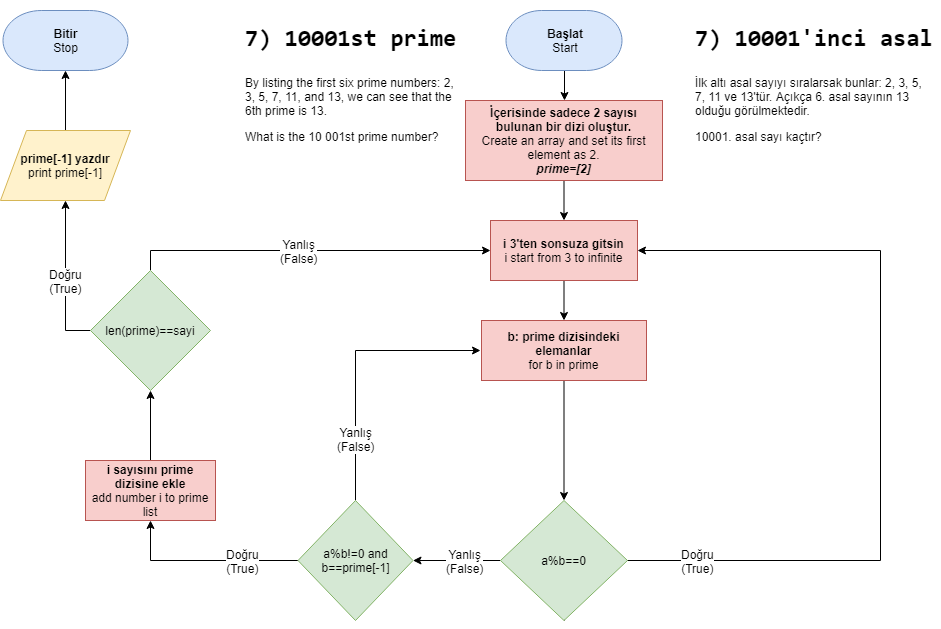
İlk altı asal sayıyı sıralarsak bunlar: 2, 3, 5, 7, 11 ve 13’tür. Açıkça 6. asal sayının 13 olduğu görülmektedir.
10001. asal sayı kaçtır?
Algoritma:
Asal sayılar, yalnızca kendisine ve 1’e kalansız bölünebilen tam sayılardır. Tanım içerisinde zaten var olduğundan 1 bu sayılara dahil değildir. En küçük asal sayı 2’dir.
- İlk asal sayımız olan 2’nin bulunduğu bir liste oluşturalım.
- İlk denenecek sayımız olan 3’ü test ederek başlayalım, her işlemin sonunda bu sayıyı arttıracağız.
- Denenecek sayımızı prime sayılar içerisindeki sayılara sırayla böldürtelim.
- Eğer liste içerisindeki asal sayılardan herhangi biri bu sayıyı bölebilirse, demek ki bu sayı asal değildir.
- Eğer hiçbir asal sayı denenen sayıyı bölemez ise, bu sayı asal demektir.
- Asal olan sayıyı listeye ekleyelim.
- Listenin uzunluğunu, yani eleman sayısını kontrol edelim.
- Eğer uzunluk 10001’e ulaşırsa programı sonlandırıp son elemanı yazdıralım.
- Eğer 10001’den küçük ise, aynı işlemleri tekrar edelim.
Akış Şeması:
Koda Dökme (Python):
prime=[2]
def kacinci_prime(sayi):
for a in range(2,56161846123184318543):
for b in prime:
if a%b==0:
break
if a%b!=0 and b==prime[-1]:
prime.append(a)
break
if len(prime)==sayi:
return(prime[-1])
break
print(kacinci_prime(10001))Algoritmanın Sıkıntıları:
Fark edeceğiniz üzere her bir asal sayı bulduğumuzda listenin uzunluğu artıyor, bu da her yeni işlemde test edilecek asal sayıların sayılarının arttığı anlamına geliyor. Program gittikçe yavaşlıyor. Mantığında kusur bulunmasa dahi, işlem kalabalığı açısından sıkıntı teşkil ediyor.