Bir Pisagor üçlüsü a < b < c ilişkisini içeren doğal sayılar olup aşağıdaki koşulu sağlamalıdır:
a^2 + b^2 = c^2
Misal, 3^2+ 4^2= 9 + 16 = 25 = 5^2.
a+b+c= 1000 koşulunu sağlayan sadece bir Pisagor üçlüsü vardır.
Bu üçlünün çarpımını bulun.
Algoritma:
İşin aslı yapmamız gereken program basit. Farklı a, b, c üçlülerini seçip bunların istediğimiz iki kriter olan a^2 + b^2 = c^2 ve a+b+c= 1000 uyup uymadığını kontrol edeceğiz. Ancak tüm sayıların tek tek denenmesi 999*999*999 işlem ve bir bu kadar da kontrol gerektireceğinden, çeşitli alt ve üst sınırlar belirlemeliyiz.
c sayısının karesi, a ve b sayılarının karelerinin toplamı olacağı için en büyük sayı c olmalı. Ayrıca a ve b sayıları c’den en az 1 sayı eksik olmalı ki, eşitlik tutarlı olsun.
1000 sayısını bir tanesi diğerlerinden daha büyük olmak üzere 3 adet yakın boyutlu sayıya bölündüğünde her ne kadar eşitliği sağlamasa da 333 333 334 olduğunu görürüz. O hâlde;
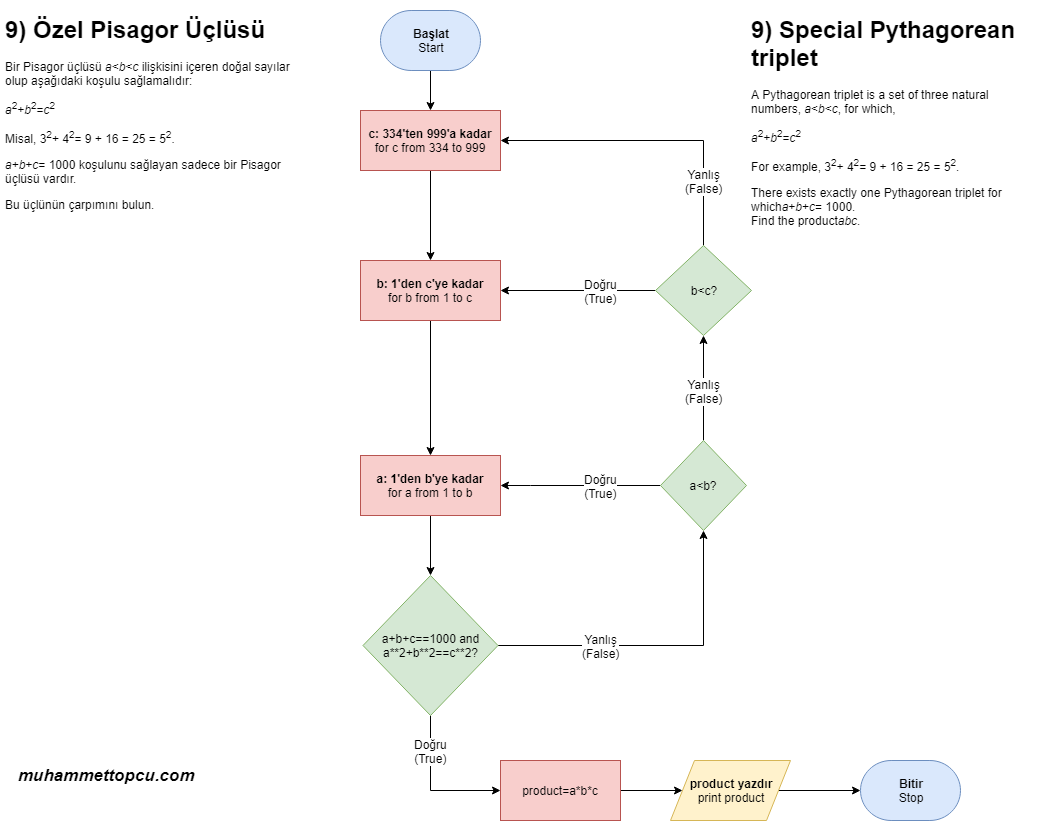
c sayısı en ufak 334 olmalıdır ki, diğer sayılardan büyük olsun. a ve b sayıları yukarıda da görüldüğü üzere eşit olabilir. a ve b sayıları c’den küçük olmalıdır.
Bunlar ışığında, sayıların aralıklarını şu şekilde belirleyebiliriz.
c: 334’ten 1000’e kadar.
b: 1’den c’ye kadar.
a: 1’den (b+1)’e kadar.
Bu üç aralığı döngüler içerisinde döndürüp, eğer yukarıda bahsettiğimiz iki durumu karşılıyorlarsa döngüyü sonlandırmalı ve a*b*c sonucunu çıkarttırmalıyız.
Akış Şeması:
Kod Dökümü:
def triplet():
for c in range(334,1000):
for b in range (1, c):
for a in range(1, b+1):
if (a+b+c)==1000 and (a**2)+(b**2)==(c**2):
return (a, b, c, a*b*c)
print(triplet())